Alberto Bañón es programador informático y colaborador habitual de la revista de ajedrez Peón de Rey.
“Lo consiguieron porque no sabían que era imposible». Jean Cocteau
El proyecto SETI analiza los datos recibidos por los radiotelescopios buscando señales de inteligencia extraterrestre. Esto requiere ordenadores de gran potencia, o muchos ordenadores trabajando a la vez. Cualquier persona con un ordenador conectado a Internet puede participar ejecutando un programa gratuito y lo hacen más de cinco millones de personas en todo el mundo.
Mi propuesta, relacionada con el Ajedrez, por una vez no tiene que ver con la inteligencia, sino con la computación distribuida, es decir, con la posibilidad de que mucha gente pueda colaborar ejecutando un programa en su ordenador personal, a diferencia del SETI, no es necesaria la conexión a Internet.
El problema del salto del caballo en un tablero de ajedrez, que consiste en recorrer las 64 casillas pasando una sólo vez por cada una de ellas está resuelto, en el sentido de que se conoce al menos una solución desde el siglo VIII, pero han sido muchos los matemáticos que han dedicado tiempo a tratar de entenderlo, entre ellos, el que algunos consideran el mayor genio matemático de la historia: Leonhard Euler (1707-1783).
Hay que destacar un método para construir soluciones desarrollado por H. C. Warnsdorff en el siglo XIX. Esté método permite encontrar una solución partiendo de cualquiera de las casillas del tablero sin más ayuda que lápiz y papel y unos pocos minutos de trabajo. La regla consiste en ir moviendo el caballo a la casilla desde la que puede realizar el mínimo número de saltos. El objetivo es evitar que el caballo se atasque porque llega a una casilla desde la que no puede mover a ninguna que no haya visitado antes. Esta regla se entiende mejor si pensamos del revés, si en lugar de a cuantas casillas podemos ir desde una dada, lo vemos como desde cuantas casillas se puede llegar a ella, que es lo mismo. Matemáticamente, diríamos que hay que visitar primero las casillas que con más probabilidad se quedarían aisladas cuando el caballo empiece a realizar su recorrido, una casilla a la que sólo se puede llegar desde dos, se quedará aislada el doble de pronto que una a la que se puede llegar desde cuatro.
Desconozco si esta era la forma de pensar de Warnsdorff, pero es la base de la aplicación informática que he desarrollado, no tanto para buscar soluciones, sino para todo lo contrario: detectar, cuanto antes, cuando se va por mal camino.
Una vez sabido que hay solución y como encontrar una fácilmente, la cuestión pasa a ser cuantas soluciones existen. En 1995 Martin Löbbing e Ingo Wegener hicieron trabajar 20 estaciones de trabajo durante cuatro meses y concluyeron que había treinta y tres billones de soluciones (33.439.123.484.294), dos años después, Brendan McKay encontró un error en la implementación de los cálculos hechos por estos y lo redujo a 13 billones (13.267.364.410.532),
¿podemos comprobarlo?
Escribir una aplicación para determinar el número exacto de soluciones es una tarea muy divertida para una aficionado al ajedrez y a la informática, por lo que no me he podido resistir. El número de recorridos posibles es una cifra totalmente fuera del alcance de nuestros ordenadores, podría ser del orden de un 1 seguido de 30 ceros (ver el anexo sobre el árbol de posibilidades), por lo que pensar en reproducirlos todos y ver cuales acaban recorriendo las 64 casillas es una quimera.
Pero no es necesario recorrerlos todos si somos capaces de saber cuándo un recorrido terminará inevitablemente atascado sin llegar a recorrer las 64 casillas, antes de que el atasco ocurra y mucho mejor cuanto antes lo anticipemos.
Aquí entra la idea de Warnsdorff, vista del revés. Durante el cálculo se mantiene una tabla con el número de casillas a las que se puede saltar desde cada una de las 64 (Warnsdorff original), pero que nosotros vemos como el número de casillas desde las que se puede saltar hasta una dada. A la tabla la llamaremos ‘Tabla W’ y a este número lo llamaremos ‘valor W’.
| 2 | 3 | 4 | 4 | 4 | 4 | 3 | 2 |
| 3 | 4 | 6 | 6 | 6 | 6 | 4 | 3 |
| 4 | 6 | 8 | 8 | 8 | 8 | 6 | 4 |
| 4 | 6 | 8 | 8 | 8 | 8 | 6 | 4 |
| 4 | 6 | 8 | 8 | 8 | 8 | 6 | 4 |
| 4 | 6 | 8 | 8 | 8 | 8 | 6 | 4 |
| 3 | 4 | 6 | 6 | 6 | 6 | 4 | 3 |
| 2 | 3 | 4 | 4 | 4 | 4 | 3 | 2 |
Tabla Warnsdorff antes de posar el caballo sobre el tablero.
El 2 en la casilla del vértice inferior izquierdo significa que desde ella se puede saltar a dos casillas, para nosotros que se puede llegar a ella desde dos casillas distintas, las marcadas en azul.
Una vez que se ejecuta el salto desde la casilla uno a la once:
| 2 | 3 | 4 | 4 | 4 | 4 | 3 | 2 |
| 3 | 4 | 6 | 6 | 6 | 6 | 4 | 3 |
| 4 | 6 | 8 | 8 | 8 | 8 | 6 | 4 |
| 4 | 6 | 8 | 8 | 8 | 8 | 6 | 4 |
| 4 | 6 | 8 | 8 | 8 | 8 | 6 | 4 |
| 4 | 5 | 8 | 8 | 8 | 8 | 6 | 4 |
| 3 | 4 | H | 6 | 6 | 6 | 4 | 3 |
| D | 3 | 4 | 4 | 4 | 4 | 3 | 2 |
Tabla W después del salto de la casilla 1 (D) a la 11 (H).
La casilla 16 ya no se podrá alcanzar desde la 1, puesto que nunca volveremos a pasar por ella y su ‘valor W’ pasa de 6 a 5.
Pues bien, en el momento que en una casilla aparezca un cero, no hay que seguir con el recorrido del caballo, aunque pueda seguir saltando, la casilla del cero nunca podrá ser alcanzada, es una isla.
| x | x | x | 4 | x | x | x | 2 |
| x | 4 | x | x | x | 5 | x | x |
| x | x | 4 | 5 | 5 | x | 4 | x |
| 4 | x | 5 | x | 6 | 4 | 5 | x |
| X | x | 4 | 5 | 3 | 5 | x | 4 |
| X | H | x | 4 | 3 | 6 | x | 3 |
| 0 | x | x | x | x | x | 4 | x |
| E | x | D | x | 3 | x | 2 | x |
La casilla 9 es una isla.
Después de 37 saltos desde la casilla 1 (E) (las casillas ocupadas están marcadas con una x), donde el último salto fue de la casilla 3 (D) a la 18 (H), la casilla 9 (0) se ha vuelto inaccesible, sólo se podía llegar a ella desde la 3. Desde la casilla 18 (H) aún se puede seguir saltando a cualquiera de las casillas en verde y desde estas a otras, ¿pero para qué?
Incorporar esta regla a la aplicación informática reduce el tiempo de cálculo a la mitad, lo que supuso una gran decepción para mí que esperaba mucho más.
La razón de este poco beneficio es que el futuro no queda predeterminado hasta muy cerca del final (el atasco). En la mayoría de los casos basta con cambiar el último movimiento realizado, o el anterior a este, para que sea posible llegar a una solución. Nunca encontraremos una regla que nos permita detenernos mientras el atasco sea evitable, lo cual tiene su miga filosófica y me recuerda la película Minority Report.
A pesar de esta decepción, o quizás por ella, seguí buscando más reglas que eviten caminar innecesariamente. Si la isla de una casilla funciona, hay que probar con la de dos casillas (desde una se llega a la otra y desde está a la primera, pero nada más) y efectivamente se reduce el tiempo un 25%, una cuarta parte del tiempo que ya se había reducido un 50%. Pasemos a la isla de tres casillas, a una se puede llegar desde y sólo desde las otras dos, por su parte, a esas dos sólo se puede llegar desde la primera (en la ‘Tabla W’ la primera tiene un 2 y las otras dos un 1). Pues hasta aquí hemos llegado, el tiempo para realizar esta comprobación es mayor que el número de saltos que nos ahorra, resultado: la aplicación va más lenta. Damos por cerrada está línea de trabajo, pero aparece una nueva.
Entre la isla de una casilla y la de dos reciprocas (las que sólo saltan entre ellas), están las casillas colgantes, a las que sólo se puede acceder desde una casilla. Esto significa que, de existir una solución, esa sería la última casilla del recorrido, tras ella no habrá donde saltar.
Si añadimos que el caballo a cada salto cambia de color (si parte de una casilla blanca irá a una negra), podemos adelantar que si el recorrido se inicia en una casilla blanca debe terminar en una negra (64 es un número par). Si la casilla colgante es del mismo color que la casilla de partida podemos dejar de saltar, no completaremos el recorrido. Esta regla consigue dividir por cinco el tiempo de cálculo, esto sí que vale la pena.
| x | x | X | 4 | x | x | x | 1 |
| x | 4 | X | x | x | 5 | x | x |
| x | x | 4 | 5 | 4 | x | D | x |
| 4 | x | 5 | x | 5 | 4 | 5 | x |
| x | x | 4 | 6 | 4 | x | x | H |
| x | 4 | 3 | 4 | 3 | 6 | x | 2 |
| 2 | x | X | x | 4 | x | 3 | x |
| E | x | 4 | x | 3 | x | 3 | x |
Empezando en la casilla 1 (E), tras el salto número 36, de la casilla 47 (D) a la 32 (H), la casilla 64 (1) queda colgando de la 54 (5). Las casillas 1 y 64 son de color negro.
Además, la casilla colgante ofrece un beneficio añadido. Si el caballo consigue dar el salto 62 sin que haya actuado el filtro de la casilla colgante, podemos asegurar que completará el recorrido hasta la 64, sólo quedan dos casillas, la del color contrario a la del salto inicial será la última y la otra la antepenúltima.
Parece tentadora la idea de exprimir aún más la casilla colgante. La idea es anotar cuando se crea una casilla colgante de las que no detiene la secuencia de saltos, porque es de distinto color que la casilla de partida (su valor W se hace igual a 1). Luego, cada vez que demos un salto, miramos si la casilla anotada está entre los posibles destinos, de ser así, la secuencia ha terminado pues la casilla colgante se convertirá en isla, o si la ocupamos en este salto, no podremos seguir saltando. Pero nuevamente es más el coste de hacer este seguimiento que el que se evita. Este filtro es casi equivalente al control de las casillas en isla, de hecho, si se implementa nunca se llegaría a tener una casilla en isla. El coste de comprobar las casillas en isla es mucho menor que el de las colgantes que no detienen la secuencia de saltos.
Llegado a este punto y tras las primeras pruebas, la velocidad con la que la aplicación encuentra las soluciones hace que parezca posible llegar a los 13 billones de McKay en un tiempo asequible, aunque estemos hablando de meses de cálculo y aquí es donde enlazamos con la idea del programa SETI.
El problema es muy fácil de dividir en cualquier número de partes independientes, a las que denominaré fracciones, que se pueden procesar en ordenadores distintos. Si se encuentra un número suficiente de colaboradores, la tarea será posible y en poco tiempo.
Antes de salir a Twitter o Facebook a solicitar ayuda, había que seguir estimando los tiempos de cálculo. En mi PC, usando un solo núcleo (core) la aplicación encuentra los primeros 1.000 millones de soluciones en una hora, pero esta velocidad se puede ir degradando con el tiempo y hacía falta saber si no va a ocurrir como Aquiles y la tortuga, que nunca pueda alcanzarla.
Tras más de 50.000 millones de soluciones encontradas se aprecian dos cosas:
Uno, la velocidad con la que se encuentran las soluciones es oscilante pero no muestra una tendencia creciente o decreciente, parece estable, lo cual es positivo.
Dos, el número de soluciones parece ser descomunalmente mayor que los 13 billones de McKay.
Esto hacía necesario acudir a la fuente de ese número. Gracias a Internet, se puede conseguir el artículo original, esta es la parte buena de Internet y la primera sorpresa es que la cifra se refiere a soluciones circulares (desde la última casilla del recorrido se puede saltar a la primera), no a todas las soluciones, si bien en todos los artículos y noticas que he visto, se cita esa cifra como la del total de soluciones. Debe ser que nos copiamos unos a otros consiguiendo eso tan conocido de que mil repeticiones de una mentira la convierten en verdad, esta es la parte mala de Internet, que todo apunta a que con el tiempo será la dominante.
Aun tratándose de soluciones circulares la cifra de McKay parece pequeña.
Después de un par de días de cálculo, para las secuencias de saltos que parten de la casilla 1 (la primera de la izquierda del jugador de blancas) la aplicación encuentra 50.000 millones de soluciones, antes de haber completado el nivel 16 de profundidad del árbol de posibilidades. Si tenemos en cuenta que en ese nivel hay 43.913.091.967 nodos, sólo hay que multiplicar para hacerse una idea de por dónde andamos, algo así como:
1.000.000.000.000.000.000.000
Una cifra mil millones de veces superior a la de McKay. De los 50.000 millones de soluciones encontrados por la aplicación, el 3% son circulares, por lo que todo apunta a que los 13 billones de MacKay son muy pocos, aún para soluciones circulares.
Lo que parece claro es que seguir adelante tratando de contar todas las soluciones es absolutamente imposible para la tecnología actual, con o sin computación distribuida.
Pero podemos tratar de estimar el orden de magnitud del número de soluciones existentes por el procedimiento esbozado de ver cuántas soluciones se encuentran a determinadas profundidades de búsqueda. Cuantas más secuencias iniciales (fracciones) se exploren mayor confianza habrá en los resultados obtenidos. Esto vuelve a reclamar el recurso a la computación distribuida, fraccionando los cálculos por el procedimiento de prefijar la casilla inicial y los dos, o tres, primeros saltos. Al final de este documento hay una lista de fracciones.
Divide y vencerás
Cualquiera que desee colaborar en este proyecto tiene que descargar la aplicación, comprobar que funciona en su PC y enviar un email a la dirección setica@ajedrezdirecto.com solicitando una, o varias fracciones de cálculo, con las que iniciar la búsqueda.
La aplicación informática sólo funciona en Windows de 64 bits y es más que recomendable que el PC disponga de más de un núcleo (core).
Para que los resultados sean significativos estimo que el número de soluciones a obtener, para cada fracción, debe ser como mínimo de 100.000 millones, o quizás de 500.000 millones. Lo que hasta ahora he observado es que el número puede variar muchísimo de una fracción a otra.
Considerando que se necesitan unas 4 horas por cada 1.000 millones de soluciones, hay que pensar en dedicar entre 400 y 2.000 horas de PC por fracción. Si el PC dispone de varios núcleos se pueden procesar varias fracciones simultáneamente.
Al probar la aplicación hay que tener en cuenta que al principio la velocidad puede ser engañosa. Sólo a partir de 1.000 millones de soluciones se estabiliza, aunque siempre cabe esperar que muestre oscilaciones. Esto es muy importante para saber si nuestro PC nos permitirá llegar a un resultado con el suficiente número de soluciones en un tiempo razonable.
Completados los cálculos habría que remitir los ficheros generados por la aplicación a la misma dirección de correo antes mencionada: setica@ajedrezdirecto.com
La aplicación informática
El programa del Camino del caballo es una aplicación de consola para Windows de 64 bits, escrita en C++, que no tiene interfaz gráfica y por lo tanto se ejecuta en lo que han dado en llamar una ventana de comandos del sistema, o sea, el antiguo DOS.
- Se puede descargar en: http://www.interajedrez.com/ccaballo/saltacaballo.zip
El archivo descargado: saltacaballo.zip se descomprime en cualquier carpeta y aparece el fichero ejecutable, Ccababllo.exe.
La forma de trabajar es muy simple: Se hace doble clic, con el ratón, sobre Ccababllo.exe y se abre una ventana. La primera vez se nos pide que introduzcamos las casillas de la secuencia inicial de partida, una por línea. Para terminar de introducir esta secuencia se pulsa retorno de carro sin escribir ninguna casilla. Por ejemplo, para empezar con los saltos:
1-18
18-33
33-50
Ya realizados, se escribe:
1 y se pulsa retorno de carro 18 y se pulsa retorno de carro 33 y se pulsa retorno de carro 50 y se pulsa retorno de carro Retorno de carro
A continuación, nos pedirá el número de soluciones a encontrar, por comodidad se aceptan puntos de millar, por ejemplo:
1.000.000.000 y se pulsa retorno de carro
Tras esto, la consola se ubicará en un lugar de su elección dentro de la pantalla y comenzará el cálculo, del que nos informa mostrando la evolución de cuatro datos, todos en la misma línea
Nivel de Profundidad actual (al llegar a cero, la búsqueda habría terminado) Número de soluciones encontradas
Tiempo consumido en segundos
Velocidad con la que se encuentran las soluciones, resultado de dividir los dos valores anteriores.
Cuando se llegue al número de soluciones que le pedimos que encontrase, o haya encontrado todas las soluciones que existen (cosa que nunca veremos), la aplicación termina, se cierra la ventana y se escriben los resultados en unos ficheros ubicados en la misma carpeta donde estaba el ejecutable sobre el que hicimos doble clic con el ratón.
Para reiniciar los cálculos volvemos a hacer doble clic con el ratón sobre el ejecutable. Esta vez no nos pedirá la secuencia inicial de saltos, sólo el número de soluciones a buscar.
Si se quiere ejecutar simultáneamente más de una copia de la aplicación hay que colocar varias copias del fichero Ccababllo.exe en carpetas distintas, para que los ficheros que se generan no entre en conflicto, cada carpeta tendrá una historia de ejecución.
Para un PC con más de un procesador, todos los actuales, se pueden procesar simultáneamente fracciones distintas aprovechando toda la capacidad de cálculo del PC.
Mi PC tiene 6 procesadores físicos (cores) cada uno con dos procesadores lógicos, por lo que podría tener buscando soluciones hasta 12 copias de la aplicación.
No hay que usar todos los procesadores del PC porque se quedaría “congelado”, la aplicación consumiría todos los recursos y no quedaría tiempo ni para el sistema operativo, siempre hay que dejar algún procesador libre, o más de uno para evitar sobrecalentamientos de la CPU.
Resultados
Cuando la aplicación termina, escribe tres ficheros en la misma carpeta donde está la aplicación:
fraccion_cc.txt
Con el resumen de los resultados en texto normal. Si el fichero existe, escribe a continuación de lo que haya, así se va formando el histórico de los cálculos. fraccion es la secuencia de saltos prefijados, como mínimo tendrá un valor entre 1 y 64 que sería la casilla inicial. Algunos ejemplos:
01_18_33_50_cc.txt 11_01_cc.txt 02_cc.txt
Cuando se reinicia la ejecución, se hace una copia de este fichero con el nombre fraccion_cc_copia.txt.
fracción_cc.csv
Con los datos básicos de la ejecución separados por punto y coma. Cada 1.000.000.000 soluciones se añade una línea como esta:
01;32;195672149;10000000;691377;15
01 es la fracción
32 es la profundidad en curso
195672149 el número de caminos intentados 10000000 el número de soluciones encontradas 691377 el número de soluciones circulares
15 el tiempo empleado en segundos.
Cuando se reinicia la ejecución, se hace una copia de este fichero con el nombre fraccion_cc_copia.csv.
nnnn_cc_fraccion.bin
Un fichero binario con el estado interno de la aplicación al terminar los cálculos para que estos puedan reiniciarse posteriormente. nnnn es un número que se va incrementando cada vez que finaliza una sesión de búsquedas.
Con independencia de que se haya limitado el cálculo a un número de soluciones determinado, en cualquier momento se puede pulsar Ctrl+C y se detendrá la búsqueda, generándose el correspondiente fichero binario para poder continuar en otro momento.
El árbol de posibilidades
Para el primer salto, dependiendo de la casilla de la que se parta, se dispone de entre 2 y 8 posibilidades. Para dos saltos, el número es 53 y para 16 asciende a 43.913.091.967.
Este número sigue creciendo con el número de saltos, pero no sabemos hasta donde. Siempre es creciente, pero según se va llegando al salto 64 su tasa de crecimiento debe aproximarse a la unidad porque cada vez quedan menos casillas libres.
Estos son los valores hasta la profundidad 16:
| Profundidad | Nodos | Base de
potencia |
Factor/Previo |
| 1 | 10 | ||
| 2 | 53 | 7,28 | 5,30 |
| 3 | 265 | 6,42 | 5,00 |
| 4 | 1.311 | 6,02 | 4,95 |
| 5 | 6.222 | 5,74 | 4,75 |
| 6 | 29.278 | 5,55 | 4,71 |
| 7 | 132.902 | 5,39 | 4,54 |
| 8 | 601.467 | 5,28 | 4,53 |
| 9 | 2.621.674 | 5,17 | 4,36 |
| 10 | 11.361.975 | 5,08 | 4,33 |
| 11 | 47.370.880 | 4,99 | 4,17 |
| 12 | 196.193.469 | 4,91 | 4,14 |
| 13 | 780.813.818 | 4,83 | 3,98 |
| 14 | 3.083.304.024 | 4,76 | 3,95 |
| 15 | 11.687.814.155 | 4,69 | 3,79 |
| 16 | 43.913.091.967 | 4,63 | 3,76 |
La ‘Base de potencia’ es el número que elevado a la profundidad da el número de nodos y Factor/Previo la relación entre el número de nodos a una profundidad respecto de la anterior. Como se ve estos valores se van reducción, ¿pero hasta dónde?
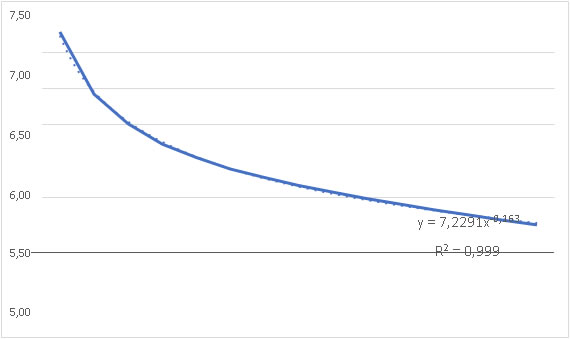
Ajustando una función potencial a los datos de la base de potencia se obtiene la siguiente ecuación:
Y = 7,2291 X -0,163
Con un excelente coeficiente de correlación R2= 0,999
Con esta fórmula, el número de nodos a la profundidad 64 es de 1 x 10 36, es decir, un 1 seguido de 36 ceros.
Esta estimación no tiene en cuenta el efecto de atenuación, antes comentado, debido a que según se avanza se van agotando las casillas disponibles
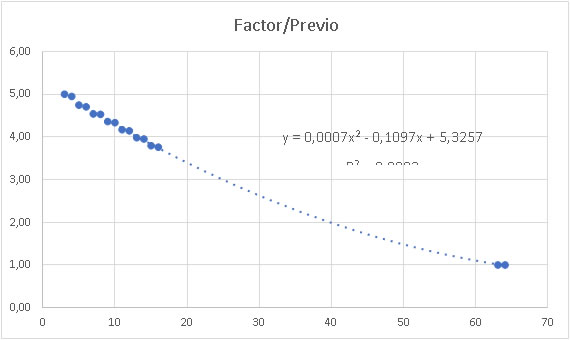
Si lo que correlacionamos es el “Factor/Previo” imponiendo que para 63 y 64 valga la unidad
Se llega a que para una profundidad de 64 el número de nodos sería de 3 x 10 25.
Fracciones de cálculo
Por motivos de simetría sólo hay que explorar los recorridos que parten de las casillas: 1, 2, 3, 4, 10, 11, 12, 19, 20, 28
En el caso de la casilla 1, hay dos posibles continuaciones para el primer salto, las casillas 11 y
- Estás son simétricas respecto de la diagonal principal por lo que sólo hay que calcular una de ellas.
Prefijando la casilla inicial y los dos primeros saltos surgen 265 fracciones:
| Casilla Inicial | Primer salto | Segundo salto |
| 1 | 18 | 35 |
| 1 | 18 | 28 |
| 1 | 18 | 12 |
| 1 | 18 | 3 |
| 1 | 18 | 33 |
| 1 | 11 | 28 |
| 1 | 11 | 21 |
| 1 | 11 | 5 |
| 1 | 11 | 17 |
| 1 | 11 | 26 |
| 10 | ||
| 2 | 19 | 36 |
| 2 | 19 | 29 |
| 2 | 19 | 13 |
| 2 | 19 | 4 |
| 2 | 19 | 9 |
| 2 | 19 | 25 |
| 2 | 19 | 34 |
| 2 | 12 | 29 |
| 2 | 12 | 22 |
| 2 | 12 | 6 |
| 2 | 12 | 18 |
| 2 | 12 | 27 |
| 2 | 17 | 34 |
| 2 | 17 | 27 |
| 2 | 17 | 11 |
| 15 | ||
| 3 | 20 | 37 |
| 3 | 20 | 30 |
| 3 | 20 | 14 |
| 3 | 20 | 5 |
| 3 | 20 | 10 |
| 3 | 20 | 26 |
| 3 | 20 | 35 |
| 3 | 13 | 30 |
| 3 | 13 | 23 |
| 3 | 13 | 7 |
| 3 | 13 | 19 |
| 3 | 13 | 28 |
| 3 | 9 | 26 |
| 3 | 9 | 19 |
| 3 | 18 | 35 |
| 3 | 18 | 28 |
| 3 | 18 | 12 |
| 3 | 18 | 1 |
| 3 | 18 | 33 |
| 19 | ||
| 4 | 21 | 38 |
| 4 | 21 | 31 |
| 4 | 21 | 15 |
| 4 | 21 | 6 |
| 4 | 21 | 11 |
| 4 | 21 | 27 |
| 4 | 21 | 36 |
| 4 | 14 | 31 |
| 4 | 14 | 24 |
| 4 | 14 | 8 |
| 4 | 14 | 20 |
| 4 | 14 | 29 |
| 4 | 10 | 27 |
| 4 | 10 | 20 |
| 4 | 10 | 25 |
| 4 | 19 | 36 |
| 4 | 19 | 29 |
| 4 | 19 | 13 |
| 4 | 19 | 2 |
| 4 | 19 | 9 |
| 4 | 19 | 25 |
| 4 | 19 | 34 |
| 22 |
| 10 | 27 | 44 |
| 10 | 27 | 37 |
| 10 | 27 | 21 |
| 10 | 27 | 12 |
| 10 | 27 | 17 |
| 10 | 27 | 33 |
| 10 | 27 | 42 |
| 10 | 20 | 37 |
| 10 | 20 | 30 |
| 10 | 20 | 14 |
| 10 | 20 | 5 |
| 10 | 20 | 3 |
| 10 | 20 | 26 |
| 10 | 20 | 35 |
| 10 | 4 | 21 |
| 10 | 4 | 14 |
| 10 | 4 | 19 |
| 10 | 25 | 42 |
| 10 | 25 | 35 |
| 10 | 25 | 19 |
| 20 | ||
| 11 | 28 | 45 |
| 11 | 28 | 38 |
| 11 | 28 | 22 |
| 11 | 28 | 13 |
| 11 | 28 | 18 |
| 11 | 28 | 34 |
| 11 | 28 | 43 |
| 11 | 21 | 38 |
| 11 | 21 | 31 |
| 11 | 21 | 15 |
| 11 | 21 | 6 |
| 11 | 21 | 4 |
| 11 | 21 | 27 |
| 11 | 21 | 36 |
| 11 | 5 | 22 |
| 11 | 5 | 15 |
| 11 | 5 | 20 |
| 11 | 1 | 18 |
| 11 | 17 | 34 |
| 11 | 17 | 27 |
| 11 | 17 | 2 |
| 11 | 26 | 43 |
| 11 | 26 | 36 |
| 11 | 26 | 20 |
| 11 | 26 | 9 |
| 11 | 26 | 41 |
| 26 | ||
| 12 | 29 | 46 |
| 12 | 29 | 39 |
| 12 | 29 | 23 |
| 12 | 29 | 14 |
| 12 | 29 | 19 |
| 12 | 29 | 35 |
| 12 | 29 | 44 |
| 12 | 22 | 39 |
| 12 | 22 | 32 |
| 12 | 22 | 16 |
| 12 | 22 | 7 |
| 12 | 22 | 5 |
| 12 | 22 | 28 |
| 12 | 22 | 37 |
| 12 | 6 | 23 |
| 12 | 6 | 16 |
| 12 | 6 | 21 |
| 12 | 2 | 19 |
| 12 | 2 | 17 |
| 12 | 18 | 35 |
| 12 | 18 | 28 |
| 12 | 18 | 3 |
| 12 | 18 | 1 |
| 12 | 18 | 33 |
| 12 | 27 | 44 |
| 12 | 27 | 37 |
| 12 | 27 | 21 |
| 12 | 27 | 10 |
| 12 | 27 | 17 |
| 12 | 27 | 33 |
| 12 | 27 | 42 |
| 31 | ||
| 19 | 36 | 53 |
| 19 | 36 | 46 |
| 19 | 36 | 30 |
| 19 | 36 | 21 |
| 19 | 36 | 26 |
| 19 | 36 | 42 |
| 19 | 36 | 51 |
| 19 | 29 | 46 |
| 19 | 29 | 39 |
| 19 | 29 | 23 |
| 19 | 29 | 14 |
| 19 | 29 | 12 |
| 19 | 29 | 35 |
| 19 | 29 | 44 |
| 19 | 13 | 30 |
| 19 | 13 | 23 |
| 19 | 13 | 7 |
| 19 | 13 | 3 |
| 19 | 13 | 28 |
| 19 | 4 | 21 |
| 19 | 4 | 14 |
| 19 | 4 | 10 |
| 19 | 2 | 12 |
| 19 | 2 | 17 |
| 19 | 9 | 26 |
| 19 | 9 | 3 |
| 19 | 25 | 42 |
| 19 | 25 | 35 |
| 19 | 25 | 10 |
| 19 | 34 | 51 |
| 19 | 34 | 44 |
| 19 | 34 | 28 |
| 19 | 34 | 17 |
| 19 | 34 | 49 |
| 34 | ||
| 20 | 37 | 54 |
| 20 | 37 | 47 |
| 20 | 37 | 31 |
| 20 | 37 | 22 |
| 20 | 37 | 27 |
| 20 | 37 | 43 |
| 20 | 37 | 52 |
| 20 | 30 | 47 |
| 20 | 30 | 40 |
| 20 | 30 | 24 |
| 20 | 30 | 15 |
| 20 | 30 | 13 |
| 20 | 30 | 36 |
| 20 | 30 | 45 |
| 20 | 14 | 31 |
| 20 | 14 | 24 |
| 20 | 14 | 8 |
| 20 | 14 | 4 |
| 20 | 14 | 29 |
| 20 | 5 | 22 |
| 20 | 5 | 15 |
| 20 | 5 | 11 |
| 20 | 3 | 13 |
| 20 | 3 | 9 |
| 20 | 3 | 18 |
| 20 | 10 | 27 |
| 20 | 10 | 4 |
| 20 | 10 | 25 |
| 20 | 26 | 43 |
| 20 | 26 | 36 |
| 20 | 26 | 11 |
| 20 | 26 | 9 |
| 20 | 26 | 41 |
| 20 | 35 | 52 |
| 20 | 35 | 45 |
| 20 | 35 | 29 |
| 20 | 35 | 18 |
| 20 | 35 | 25 |
| 20 | 35 | 41 |
| 20 | 35 | 50 |
| 40 | ||
| 28 | 45 | 62 |
| 28 | 45 | 55 |
| 28 | 45 | 39 |
| 28 | 45 | 30 |
| 28 | 45 | 35 |
| 28 | 45 | 51 |
| 28 | 45 | 60 |
| 28 | 38 | 55 |
| 28 | 38 | 48 |
| 28 | 38 | 32 |
| 28 | 38 | 23 |
| 28 | 38 | 21 |
| 28 | 38 | 44 |
| 28 | 38 | 53 |
| 28 | 22 | 39 |
| 28 | 22 | 32 |
| 28 | 22 | 16 |
| 28 | 22 | 7 |
| 28 | 22 | 5 |
| 28 | 22 | 12 |
| 28 | 22 | 37 |
| 28 | 13 | 30 |
| 28 | 13 | 23 |
| 28 | 13 | 7 |
| 28 | 13 | 3 |
| 28 | 13 | 19 |
| 28 | 11 | 21 |
| 28 | 11 | 5 |
| 28 | 11 | 1 |
| 28 | 11 | 17 |
| 28 | 11 | 26 |
| 28 | 18 | 35 |
| 28 | 18 | 12 |
| 28 | 18 | 3 |
| 28 | 18 | 1 |
| 28 | 18 | 33 |
| 28 | 34 | 51 |
| 28 | 34 | 44 |
| 28 | 34 | 19 |
| 28 | 34 | 17 |
| 28 | 34 | 49 |
| 28 | 43 | 60 |
| 28 | 43 | 53 |
| 28 | 43 | 37 |
| 28 | 43 | 26 |
| 28 | 43 | 33 |
| 28 | 43 | 49 |
| 28 | 43 | 58 |
| 48 |
Si se prefijan los tres primeros saltos el número de fracciones es de 1.311, si cuatro 6.222, con cinco 29.278 y para seis 132.902
Para un número de participantes en torno al centenar, se usarían las fracciones de dos saltos.